- CFA Exams
- 2023 Level I > Topic 1. Quantitative Methods > Reading 4. Common Probability Distributions
- 7. The Standard Normal Distribution
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 7. The Standard Normal Distribution
The way to get around this problem is to standardize a normal random variable, which involves converting it to a general scale for which probability tables exist.
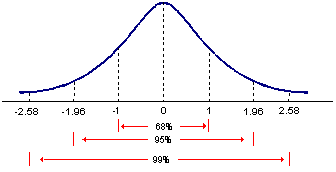
The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1. It is denoted as N(0,1). Below are some confidence intervals for the standard normal distribution:
There is an unlimited number of normal distributions, each with a different mean or standard deviation. Therefore, it's impractical to provide a table of probabilities for each combination of mean and standard deviations. However, the actual distribution for a normal random variable to a standard normal distribution can be standardized. Normal distributions can be transformed to standard normal distributions by the formula:

where X is a score from the original normal distribution, μ is the mean of the original normal distribution, and σ is the standard deviation of original normal distribution.
The standard normal distribution is sometimes called the z distribution. A z score (also called z-value or z-statistic) is the distance between a selected value (X) and the population mean, divided by the population standard deviation. It is in fact a standard normal random variable. For instance, if a person scored 70 on a test with a mean of 50 and a standard deviation of 10, that person scored 2 standard deviations above the mean. Converting the test scores to z scores, an X of 70 would be: z = (70 - 50) / 10 = 2.
So, a z score of 2 means the original score was 2 standard deviations above the mean. Note that the z distribution will only be a normal distribution if the original distribution (X) is normal.
Example
The rates of return on the assets in a portfolio are normally distributed, with a mean of 20% and a standard deviation of 12%. What's the probability that the return on an asset falls between -3.52% and 50.96%?
Solution:
- If the return on the asset is -3.52%, its z-value is z = (-3.52% - 20%)/12% = -1.96.
- If the return on the asset is 50.96%, its z-value is (50.96% - 20%)/12% = 2.58.
- Recall that a normal distribution is symmetrical. The 95% confidence interval is -1.96 to 1.96. The 99% confidence interval is -2.58 to 2.58. The probability of z-value falling between -1.96 and 2.58 is 95%/2 + 99%/2 = 97%.
How to Use the Z-Table
The z-table gives cumulative probability values for a Z-graph (or standard normal distribution). In other words, by looking up a particular z-value, the probability of all values smaller than this value can be found.
Recall that a cumulative distribution function gives probabilities of the form: P (X < x), that is, probabilities that are less than the value being examined.
In the same way, the table gives probabilities of the form: P(Z < z), that is, probabilities that are less than the z-value being looked up or calculated.
The first column, headed z, ranges from 0.0 to 4.0. Across the top, the values range from 0.00 to 0.09. These values allow a person to look up any z-value to two decimal places. The vertical column gives the value to one decimal place and the horizontal row gives the values in the second decimal position. So, for example, if you want to look up z = 0.26, you would go to the row that starts 0.2 and go to the column headed 0.06. You can then read the value 0.6026, which means that 60.26% of z-values or z-scores are less than 0.26.
So, the body of the table (the middle part) gives probabilities (or areas under the graph); hence; all the values in the body of the table lie between 0 and 1. Actually, they lie between 0.5 and 1, because the table starts considering z-values from the point 0.

You can see that 60.26% of the area under the graph lies to the left of the point z = 0.26. Therefore, 39.74% of the area lies to the right of this point. Because areas under continuous graphs give probabilities, you can also say that: P(Z < 0.26) = 0.6026.
At this point, you might have a question. Z-scores generally range from -4 to 4, but the table has no negative values. Why not?
To answer this, recall that a normal distribution is symmetrical about its mean; this fact can be used to calculate probabilities for negative z-values very easily.
Example
Take the point z = 1.83. The table shows the area to the left of 1.83 as 0.9664. The area to the right of 1.83 is therefore 1- 0.9664 = 0.0336. Because of symmetry, the area to the right of 1.83 is the same as the area to the left of -1.83. So, if the area to the left of a negative value is required, simply take 1 - the area to the left of the equivalent positive value. Problem solved.
Continuing with this example, the area to the left of -1.83 is 0.0336, which is the probability of obtaining a z-score smaller than -1.83.
A portion of the z-table is presented below. (N(z) represents the cumulative probability distribution for a standard random variable Z):

Example
Suppose that you want to find the probability that a standard normal variable is less than or equal to 1.01. In the z-table, go down the column headed by the letter z to 1.00. Move to the right and read the entry under the column headed 0.01. It's 0.8438. That is, P(Z ≤ 1.01) = 0.8438 or 84.38%, and P(Z ≥ 1.01) = 15.62%.

A standard normal distribution is symmetrical with a mean of 0. Therefore, P(Z ≤ 0) = 50% ==> P(0 ≤ Z ≤ 1.01) = 0.8438 - 0.5 = 34.38%.
Comprehensive Example
The heights of people in a city are normally distributed with mean 170 cm and standard deviation 10 cm. Calculate the probability that a randomly chosen person from this population has a height that is:
- less than 180 cm
- less than 150 cm
- greater than 175 cm
- between 160 cm and 185 cm
- greater than 150 cm
Because there is a normal distribution that is not standardized, it is important to standardize each value before looking up answers in a z-table. Let X = the heights of people in the population.
1. You want P(X < 180). Standardizing gives P(Z < (180-170)/10) = P(Z < 1). From tables, look up 1.00 and you get 0.8413. So, the answer is 0.8413.

2. You want P(X < 150). Standardizing gives P(Z < (150-170)/10) = P(Z < -2). Recall that this probability is the same as P(Z > 2), due to the symmetrical nature of the normal distribution. From tables, look up 2.00 and you get 0.9772. This is the probability that Z<2, so 1 - 0.9772 = 0.0228 is the probability that we want. So, the answer is 0.0228.

3. You want P(X > 175). Standardizing gives P(Z > (175-170)/10) = P(Z > 0.5). From tables, look up 0.50 and you get 0.6915. This is the probability that Z < 0.5, so 1-0.6915 = 0.3085 is the probability that we want. So, the answer is 0.3085.

4. You want P(160 < X < 185). Standardizing gives P(-1 < Z < 1.5). In order to find a region like this, note that this region can be written as P(Z < 1.5) - P(Z < -1). From tables, look up 1.50 and you get 0.9332. This is the probability that Z < 1.5. To find P(Z < -1), look up 1.00 and you get 0.8413. 1 - 0.8413 = 0.1587 is therefore the probability you want. So, the answer is 0.9332 - 0.1587 = 0.7745.

5. You want P(X > 150). Standardizing gives P(Z > (150-170)/10) = P(Z > -2). Using symmetry, P(Z > -2) = P(Z < 2). From tables, look up 2.00 and you get 0.9772. So, the answer is 0.9772.

Notes:
- These examples encompass the different types of regions you can get. Familiarize yourself with how each region works. If you can do these five examples, you know that you understand this process well.
- Always standardize before going to tables.
- As a check, if the region you are looking for is bigger than half the area under the graph, the answer will be bigger than 0.5 and vice versa. Verify this factor to make sure that you haven't made a silly mistake.
- It is possible to work in reverse. For example, a standardized value can be converted back to an X value using X = σZ + μ. So, in the height example above, a standardized value of 3 is equivalent to an X value of 10 x 3 + 170 = 200 cm.
Practice Question 1
True or False? If false, correct the statement.A confidence interval estimate for a parameter is used to eliminate the element of chance from estimation.Correct Answer: False
The confidence interval is used to acknowledge the element of chance in estimation.
Practice Question 2
An investor estimated the mean return of a portfolio at 12% and the standard deviation at 16%. What is the 95% confidence interval for the mean return on this portfolio?A. [-19.36%, 43.36%]
B. [-14.32%, 18.32%]
C. [-5.42%, 18.58%]Correct Answer: A
The relevant confidence interval is given by X-bar +- 1.96 x 16.
Practice Question 3
An analyst wants to calculate a 95% confidence interval for the weighted-average of the projected mean return of a portfolio he manages. His latest calculations show that this portfolio has a weighted-average return of 8% and a variance of 36. What is the 95% confidence interval?A. [-62.56%, 78.56%]
B. [-3.76%, 19.76%]
C. [-1.87%, 17.87%]Correct Answer: B
The variance is 36, which corresponds to a standard error of 6%. The 95% confidence interval is given by: X-bar ± 1.96 x s = 8 ± 1.96 x 6.
Practice Question 4
For a data collection, if a score has a z-score of 1.5, then ______A. the score is 1.5 standard deviations above the mean.
B. the score is better than 15% of the scores in the data collection.
C. the score is 1.5 standard deviations below the mean.Correct Answer: A
A z-score provides the number of standard deviations an x-score is above or below the mean. A z-score of 1.5 informs you that the piece of data is 1.5 standard deviations above the mean.
Practice Question 5
For a set of data with mean 70 and standard deviation 10, the z-score for 62 is ______.A. 0.8
B. -0.8
C. -8 Correct Answer: B
The z-score for a piece of data is z = (score - mean)/std dev. For an x-score of 62, we have z = (62 - 70)/10 = -0.8. So, 62 has a z-score of -0.8.
Practice Question 6
Which of the following statements is incorrect?A. A standard normal random variable has a variance of 1.0 and is centered at zero.
B. A standard normal random variable has a mode of 1.0.
C. Any normal random variable can be converted to a standard normal distribution.Correct Answer: B
The mode of a standard normal distribution is 0.0.
Practice Question 7
A computed z-value of -1.75 tells us ______A. the value -1.75 has a standard normal distribution.
B. the mean of the distribution is -1.75.
C. the standard deviation of the distribution is -1.75.
D. none of the aboveCorrect Answer: D
A z-value of -1.75 tells us that the observation is 1.75 standard deviations below the mean.
Practice Question 8
The daily sales at a certain cafe follow a normal distribution with a mean of $1,060 and a standard deviation of $310. What is the z-value associated with daily sales of $1,711?A. -2.10
B. 2.10
C. 36.97Correct Answer: B
The z-value is computed as: z = (x - μ)/σ = 2.10.
Practice Question 9
Suppose a set of data has a mean of 52 and a standard deviation of 6. According to Chebyshev's Theorem, at least what percentage of the data lies between 40 and 64? If the data is normally distributed, about what percentage of the data lies between 40 and 64, according to the Empirical Rule?A. 0%, 68%
B. 75%, 95%
C. 94%, 100%Correct Answer: B
Practice Question 10
As part of a promotion for a new type of cracker, free trial samples are offered to shoppers in a local supermarket. The probability that a shopper will buy a packet of crackers after testing the free sample is 0.20. Different shoppers can be regarded as independent trials. Let X be the number among the next 100 shoppers who buy a packet of the crackers after tasting a free sample. The probability that fewer than 30 buy a packet after tasting a free sample is approximately ______.A. 0.20
B. 0.9938
C. None of the aboveCorrect Answer: B
X, the number among the next 100 shoppers who buy a packet of the crackers after tasting a free sample, has approximately an N(20, 4) distribution. You need to evaluate P(X <= 30), which equals 0.9938.
Practice Question 11
The lifetime of a 2-volt non-rechargeable battery in constant use has a normal distribution with a mean of 516 hours and a standard deviation of 20 hours. The proportion of batteries with lifetimes exceeding 520 hours is approximately ______.A. 0.20
B. 0.5793
C. 0.4207Correct Answer: C
The z-score corresponding to 520 is (520 - 516)/20 = 0.2. The area to the right is 1 - 0.5793 = 0.4207, which corresponds to the proportion with lifetimes exceeding 520.
Practice Question 12
The random variable X denotes the time taken for a computer link to be made between the terminal in an executive's office and the computer at a remote factory site. It is known that X has a normal distribution with a mean of 15 seconds and a standard deviation of 3 seconds. P(X > 20) has value (choose the closest option) ______.A. 0.048
B. 0.952
C. 1.67Correct Answer: A
To compute P(X > 20), we must first find the z-score of 20. We compute this z-score as z-score = (20 - μ)/σ = (20 - 15)/3 = 1.67.
Then we need to find the area to the right of this z-score. From the z-score table, we find that the area to the left of 1.67 is 0.9525. To find the area to the right of 1.67, we simply subtract 0.9525 from 1, which yields 0.0475, which, after rounding, is 0.048.
Practice Question 13
For x, a random variable from a normal distribution with mean 40 and standard deviation 5, P(x > 20) = ______ (to the nearest 0.1%).A. 0+
B. 95%
C. 1-Correct Answer: C
The z-score for 20 is (20 - 40)/5 = -4. Reading the normal table, the smallest entry is -3.09 and its value is 0.0010. So, P(x < 20) = 0+. Thus, P(x > 20) = 1 - 0+ = 1-. That is, when rounded to the nearest 0.1%, the answer is 100%, but because 1 holds a special place in probability (indicating a must-happen event), we report 1-.
Practice Question 14
For x, a random variable from a normal distribution with mean 40 and standard deviation 5, P(28 < x < 38) = ______ (to nearest 0.1%).A. 35.3%
B. 34.5%
C. 33.6%Correct Answer: C
The z-score for 38 is (38 - 40)/5 = -0.4. The table value for -0.4, P(x < 38), is 0.3446. The z-score for 28 is -1.2 and the table value is 0.0082.
P(28 < x < 38) = 0.3446 - 0.0082 = 0.3364 or 33.6% (to the nearest 0.1%).

Practice Question 15
For the MRC test, with scores normally distribution with m = 70 and s = 5, the cutoff for the bottom 10% is ______.A. 60
B. 68.72
C. 63.6Correct Answer: C
We start by looking in the middle of the table for 0.1. The row and column values are -1.2 and 0.08. So, the x-score that is 1.26 standard deviations below the mean cuts off the bottom 10%. This x-score, 70 - 1.28(5), is 63.6. Note that P(x < 63.6) = 0.1.

Practice Question 16
The daily sales at a certain shop follow a normal distribution with a mean of $1,060 and a standard deviation of $310. What is the probability that the daily sales are less than $409?A. 0.0179
B. 0.4821
C. 0.5179Correct Answer: A
The z-value corresponding to $409 is computed as: z = (409 - 1060)/310 = -2.10. From z-table P(Z <= -2.10) = 0.0179, P(Sales <= 409) = 0.0179.
Practice Question 17
The daily sales at a certain cafe follow a normal distribution with a mean of $1,060 and a standard deviation of $310. What is the probability that the daily sales are between $471 and $1,401?A. 0.4713
B. 0.3643
C. 0.8356Correct Answer: C
The z-value corresponding to $471 is computed as: z = (471 - 1060)/310 = -1.90, and P(Z<= -1.90) = 0.0287.
The z-value corresponding to $1,401 is computed as: z = (1401 - 1060)/310 = 1.10, and P(Z<= 1.10) = 0.8643.
The probability that sales are between $471 and $1,401 is the difference in the cumulative probability values: 0.8643 - 0.0287 = 0.8356.
Practice Question 18
The amount of fill in a certain brand of bottled water is normally distributed with a mean of 16 ounces and a standard deviation of .25 ounce. What is the probability that a bottle has more than 16.25 ounces?A. 0.1587
B. 0.3413
C. 0.6587Correct Answer: A
The z-value corresponding to 16.25 is computed as: z = (16.25 - 16)/0.25 = 1.00. P(Z>=1.00) = 1 - P(Z <=1.00) = 1 - 0.8413 = 0.1587
Practice Question 19
A standard normal distribution has ______.A. a mean equal to its variance
B. a mean of 1 and a variance of 1
C. a mean of 0 and a variance of 1Correct Answer: C
Practice Question 20
A bell-shaped, symmetrical frequency distribution has a mean of 45. If 95% of the observations on the variable fall between 30 and 60, the standard deviation of the variable is ______.A. 5.00
B. 7.50
C. 15.0Correct Answer: B
95% of the observations in a bell-shaped, symmetrical frequency distribution lie within approximately 2 standard deviations of the mean. The standard deviation is then (45-30)/2 = 7.50.
Practice Question 21
The distribution of the annual incomes of a group of middle management employees approximated a normal distribution with a mean of $37,200 and a standard deviation of $800. About 68 percent of the incomes lie between what two incomes?A. $34,800 and $39,600
B. $36,400 and $38,000
C. $35,600 and $38,800Correct Answer: B
0.68/2 = 0.34. The z-value for 0.34 is 1. x = u ±- z*sigma. So, x = 37200 ± 1*800. So, x is between 36,400 and 38,000.
Practice Question 22
The lifetime of a 2-volt non-rechargeable battery in constant use has a normal distribution with a mean of 516 hours and a standard deviation of 20 hours. Ninety percent of all batteries have a lifetime less than ______.A. 517.28 hours
B. 536.00 hours
C. 541.60 hoursCorrect Answer: C
The z-value corresponding to the proportion 0.9000 is 1.28. We need to use the formula x = u + z σ, where z = 1.28, to get the correct answer, or x = 516 + 1.28 x 20 = 541.6.
Practice Question 23
Daily travel expenses for H&J Employees are normally distributed with a mean of $250 and a standard deviation of $38. Q1 for this distribution is ______.

A. $224.54
B. $275.46
C. $288.00Correct Answer: A
We want the cutoff for the bottom 25% of the distribution. The row and column for a table value of 0.25 is row 0.6 and column of 0.07. The x-score for a z-score of -0.67 is 250 - 0.67(38) = 224.54. So, Q1 = $224.54.
Practice Question 24
The distribution of lifetimes for a certain type of light bulb is normally distributed with a mean of 1000 hours and a standard deviation of 100 hours. Find the 33rd percentile of the distribution of lifetimes.A. 560
B. 1044
C. 956Correct Answer: C
P(z<=?) = 0.33
z = -0.44
-0.44 = (x-1000)/(100)
x = -44 + 1000 = 956
Practice Question 25
Suppose you were told that scores on an examination were converted to standard scores with a mean of 500, range of 800, and a standard deviation of 100. A person with a score of 600 has performed better than what percentage of the persons taking the test?A. 57 percent
B. 97.5 percent
C. 84 percentCorrect Answer: C
Z = (X - MU)/Standard Deviation
Z = (600 - 500)/100 = 1
Area between Z and Mean = 0.3413
Area to Left of Z = 0.5 + 0.3413 = 0.8413
Percentile Rank = 100*0.8413 = 84.13
Therefore, this person has performed better than 84% of the people who took the test.
Practice Question 26
Consider a normal distribution with MU = 67 and SIGMA2 = 144. If each score is raised by 7 points, what percentage of the new scores is less than 74?A. 72%
B. 88%
C. 50%Correct Answer: C
Since each score has been raised by 7 points, the mean will also be raised by 7 points. The new mean is 74. 50% of the scores will be less than the mean of a normal distribution.
Practice Question 27
The seasonal output of a new experimental strain of pepper plants was carefully weighed. The mean weight per plant is 15.0 pounds and the standard deviation of the normally distributed weights is 1.75 pounds. Of the 200 plants in the experiment, how many produced peppers weighing between 13 and 16 pounds?A. 118
B. 100
C. 197Correct Answer: A
[z = (x-u)/σ. z1 = (13 - 15)/1.75 = -1.1429 and z2 = (16 - 15)/1.75 = 0.5714]
The respective areas for those z-values are 0.3729 and 0.2157. Since they are on opposite sides of the mean, we add them to find the area in between, which is 0.5886. Therefore, 0.5886*200 = 118.
Practice Question 28
A bell-shaped, symmetrical frequency distribution has a mean of 10. If 16% of the observations in the distribution are negative, what is the coefficient of variation of X?A. 0.1
B. 1.0
C. 10.0Correct Answer: B
The fraction of observations that are less than zero equals 16%; i.e., the fraction of observations that are less than (mean - 10) equals 16% (given). Since the distribution is symmetrical about the mean, this implies that the fraction of observations that are more than (mean + 10) also equals 16%. Thus, the fraction of the observations lying between 0 and 20 equals 1-0.16-0.16 = 0.68. For a bell-shaped, symmetrical frequency distribution, 68% of the observations lie within one standard deviation of the mean. Hence, the standard deviation of the distribution equals 10. The coefficient of variation is then equal to standard deviation/mean = 10/10 = 1.
Practice Question 29
What is the area under the normal curve between z = 1.0 and z = 2.0?A. 0.4772
B. 0.1359
C. 0.7408Correct Answer: B
From the z-tables, z = 1 is 0.3413 and z = 2 is 0.4772. So, the area between is 0.4772 - 0.3413 = 0.1359.
Practice Question 30
A study of a company's practice regarding the payment of invoices revealed that on average, an invoice was paid 20 days after it was received. The standard deviation equaled five days. Assuming that the distribution is normal, what percent of the invoices were paid within 15 days of receipt?A. 34.13%
B. 37.91%
C. 15.87%Correct Answer: C
z = (x-μ)/σ = (15 - 20)/5 = -1.0. z = 1 is 0.8413. 1.0 - 0.8413 = 0.1587
Practice Question 31
We would like to refer all probability statements to one set of normal probability values. The distribution that fills this role is known as the ______.A. binomial distribution
B. standard normal distribution
C. continuous uniform distributionCorrect Answer: B
The standard normal distribution is the distribution that occurs when a normal random variable has a mean of zero and a standard deviation of one.
Practice Question 32
An analyst who manages an equity portfolio forecasts a portfolio return of 10% and estimates a standard deviation of annual return of 18%. What is the probability that the portfolio return will be between 10% and 20%?A. 18.7%
B. 19.67%
C. 21.2%Correct Answer: C
The probability is 21.2% that the portfolio return will be between 10% and 20%:
Z = (X - X-bar)/σ
X = 10%: Z = (10% - 10%) /18% = 0.
X = 20%: Z = (20% - 10%) /18% = 0556.
A Z-value of 0 gives us 0.5 on the table. A Z-value of 0.56 gives us 0.7123 on the table.
The solution is 0.7123 - 0.50 = 0.2123 = 21.23%.
Practice Question 33
What is the probability that a value of 30 or more will be observed from a normal distribution with a mean of 15 and standard deviation of 25?A. 50%
B. 27.4%
C. 60%Correct Answer: B
We need to calculate the standard normal variance, z = (30 - 15)/25 = 0.60. From the standard normal tables, Prob(z <= 0.60) = 0.7257. Thus, Prob(z >= 0.60) = 1 - 0.7257 = 0.2743, or 27.4%.
Practice Question 34
A standard normal distribution (Z-distribution) has ______.A. mean 1 and standard deviation 0
B. mean 1 and standard deviation 1
C. mean 0 and standard deviation 1Correct Answer: C
A standard normal distribution is the distribution that occurs when a normal random variable has a mean of zero and a standard deviation of one.
Practice Question 35
An analyst determines that approximately 99% of the observations of daily sales for a company are within the interval from $230,000 to $480,000 and that daily sales for the company are normally distributed. The standard deviation of daily sales (in $) for the company is closest to ______.A. 41,667
B. 62,500
C. 83,333Correct Answer: A
Given that sales are normally distributed, the mean is centered in the interval.
Mean = ($230,000 + 480,000) / 2 = $355,000. 99% of observations under a normal distribution will be plus/minus three standard deviations. Thus, ($355,000 - $230,000)/3.0 = $41,667. It is also the case that ($480,000 - $355,000)/3.0 = $41,667.

Study notes from a previous year's CFA exam:
7. The Standard Normal Distribution