- CFA Exams
- 2026 Level II
- Topic 9. Portfolio Management
- Learning Module 40. Using Multifactor Models
- Subject 1. Arbitrage Pricing Theory
Seeing is believing!
Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.
Subject 1. Arbitrage Pricing Theory PDF Download
Both the market model and CAPM are single factor models. The common, single factor is the return on the market portfolio. Multifactor models describe the return on an asset in terms of the risk of the asset with respect to a set of factors. Such models generally include systematic factors, which explain the average returns of a large number of risky assets. Such factors represent priced risk, risk for which investors require an additional return for bearing.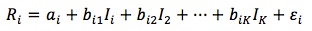
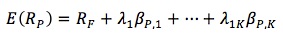
R(RP) = the expected return to portfolio p
RF = risk-free rate
λj = the risk premium for factor j. Each λ stands for the expected risk premium associated with each risk factor. Each λj equals the risk premium for a portfolio (a pure factor portfolio) with factor sensitivity of 1 to factor j and a sensitivity of 0 to all other factors.
βP,j = the sensitivity of the portfolio to factor j. Note that the APT does not require that one of the risk factors is the market portfolio.
K = the number of factors.
An arbitrage arises if an investor can construct a zero investment portfolio with a sure profit. Since no investment is required, an investor can create large positions to secure large levels of profit. In efficient markets, profitable arbitrage opportunities will quickly disappear.
The arbitrage pricing theory (APT) describes the expected return on an asset (or portfolio) as a linear function of the risk of the asset with respect to a set of factors.
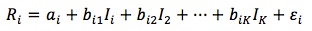
bik is the sensitivity of the return on asset I to the return to factor k, k = 1, 2, ... K
Both CAPM and APT describe what the expected return on a risky asset should be in equilibrium given its risk. The APT makes less strong assumptions.
- A factor model describes asset returns. The APT model, however, does not tell us which factors are relevant.
- The returns of a security are based on the systematic risk exposure of the security. This means that asset-specific risk can be eliminated. APT applies to well-diversified portfolios.
- No arbitrage opportunities exist among well-diversified portfolios. APT does not rely on the existence of a market portfolio. It is based purely on no-arbitrage conditions.
Remember the assumptions of CAPM? One investment period, rational investors, risk averse, homogeneous expectations, infinitely divisible investments, price takers, etc.
Consider a world where investors are broadly diversified, but there are multiple sources of risk in the economy. Rather than caring solely about the market portfolio, investors are concerned with many factors, including shifts in stock index levels, interest rates, inflation, and changes in GDP or other broad macro-economic factors difficult to purge from a portfolio through diversification.
If the above assumptions hold true, the APT equation becomes:
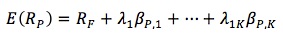
where:
R(RP) = the expected return to portfolio p
RF = risk-free rate
λj = the risk premium for factor j. Each λ stands for the expected risk premium associated with each risk factor. Each λj equals the risk premium for a portfolio (a pure factor portfolio) with factor sensitivity of 1 to factor j and a sensitivity of 0 to all other factors.
βP,j = the sensitivity of the portfolio to factor j. Note that the APT does not require that one of the risk factors is the market portfolio.
K = the number of factors.
This equation shows that the expected return on any well-diversified portfolio is linearly related to the factor sensitivities of that portfolio.
CAPM versus APT
Like CAPM, the basic concept of APT is that differences in expected return must be driven by differences in non-diversifiable risk. That is, the returns of a security are based on the systematic risk exposure of the security, as opposed to the total risk. However, the APT is not an equilibrium concept. It does not rely on the existence of a market portfolio. It is based purely on no-arbitrage conditions.
Compared to CAPM, APT is a broader-based theory, indicating that all the systematic factors may not be represented in the single market factor represented by the CAPM. The APT model requires fewer assumptions and considers multiple factors to help explain the risk of an asset.
The APT model is a useful tool for building portfolios adapted to particular needs. For example, suppose a major oil company wanted to create a pension fund portfolio that was insulated from shock to oil prices. APT allows the manager select a diversified portfolio of stocks with low exposure to inflation shocks (oil prices are correlated to inflation). If the CAPM is a "one size fits all" model of investing, the APT is a "tailor-made suit." In the APT world, people can and do have different tastes and care more or less about specific factors.
CAPM can be considered a special case of APT where there is only one risk factor: the market portfolio.
User Contributed Comments 3
| User | Comment |
|---|---|
| DariSH | How come APT is based purely on no-arbitrage conditions? |
| Oksanata | no, APT is also based on non-systematic risk elimination and no number of factors specified. No-arbitrage conditions are the conditions of financial markets equilibrium..so if these 3 conditions hold, the equation of E(Rp)=Rf+LAMBDA 1*BETA p,1+...+LAMBDA k*BETA p,k holds...,i.e. APT holds.. |
| berns23 | Carhart 4 factor model is missing here |

Thanks again for your wonderful site ... it definitely made the difference.

Craig Baugh
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add