When a coin is flipped, the outcome is either heads or tails. When a magician guesses the card selected from a deck, the magician can either be correct or incorrect. When a baby is born, the baby is either born in the month of March or is not. In each of these examples, an event has two mutually exclusive possible outcomes. For convenience, one of the outcomes can be labeled "success" and the other outcome "failure." If an event occurs N times (for example, a coin is flipped N times), then the binomial distribution can be used to determine the probability of obtaining exactly r successes in the N outcomes.

A Bernoulli trial is an experiment with two outcomes, which can represent success or failure, up move or down move, or another binary outcome. As one of these two outcomes must definitely occur, that is, they are exhaustive, and also mutually exclusive, it follows immediately that the sum of the probabilities of a "success" and a "failure" is 1.

A binomial random variable X is defined as the number of successes in n Bernoulli trials. The assumptions are:

• The probability (p) of success is constant for all trials. Similarly, the failure probability 1 - p stays constant throughout the experiment.
• The trials are independent. Thus, the outcome of one trial does not in any way affect the outcome of any subsequent trial.
• The sampling is done with replacement. This means that once an outcome has occurred, it is not precluded from occurring again.

The binomial probability for obtaining r successes in n trials is:

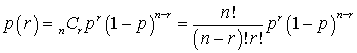
where p(r) is the probability of exactly r successes, n is the number of events, and p is the probability of success on any one trial. This formula assumes that the events are:

• dichotomous (fall into only two categories)
• mutually exclusive
• independent
• randomly selected

To remember the formula, note that there are three components:

• n!/[(n-r)! x r!]. This indicates the number of ways r successes can be achieved and n - r failures in n trials, where the order of success or failure does not matter. This is the combination formula.
• p^r. This is the probability of getting r consecutive success.
• (1 - p)^n-r. This is the probability of getting n - r consecutive failures.

The values for n and p will always be given to you in a question; their values will never have to be guessed.

Consider this simple application of the binomial distribution. What is the probability of obtaining exactly 3 heads if a coin is flipped 6 times? For this problem, n = 6, r = 3, and p = 0.5, =>p(3) = {6!/[(6 - 3)! x 3!]}0.5³(1 - 0.5)^6-3 = 0.3125.

Often the cumulative form of the binomial distribution is used. To determine the probability of obtaining 3 or more successes with n = 6 and p = 0.3, compute p(3) + p(4) + p(5) + p(6).

For a single Bernoulli random variable, Y, which takes on the value 1 with probability p and the value 0 with probability 1 - p, the mean is p and the variance is p(1 - p).

Every random variable has a mean and a variance associated with it. A general binomial random variable, B(n, p), is the sum of n Bernoulli random variables, and so the mean of a B(n, p) random variable is np. Given that a B(1, p) variable has variance p(1 - p), the variance of a B(n, p) random variable is n times that value, or np(1 - p), using the independent assumption.

For example, for a B(n = 5, p = 0.10) random variable, the expected number of successes is 5 x 0.1 = 0.5 with a standard deviation of (5 x 0.1 x 0.9)^1/2 = 0.67.

Practice Question 1

Find the probability of having exactly four girls in seven births. Assume no multiple births and that male and female births are equally likely and independent.

A. 0.063
B. 0.571
C. 0.273

Correct Answer: C

₇C₄ x (0.5)⁴ x (0.5)^(7-4) = 0.273

Practice Question 2

Suppose that 20% of all drivers come to a complete stop at an intersection having flashing red lights in all directions when there are no other cars visible. What is the probability that, of 15 randomly selected drivers coming to the intersection under these conditions, exactly 5 will come to a complete stop?

A. 0.103
B. 0.188
C. 0.812

Correct Answer: A

n = 15 and pai = 0.2, so p(5) = 15!/[5! x 10!] x (0.2)⁵ x 0.8¹⁰ = 0.103.

Practice Question 3

A set of four cards consists of two red cards and two black cards. The cards are shuffled thoroughly, and I am dealt two cards. I count the number of red cards X in these two cards. The random variable X has which of the following probability distributions?

A. The binomial distribution with parameters n = 4 and p = 0.5
B. The binomial distribution with parameters n = 2 and p = 0.5
C. None of the above

Correct Answer: C

Because two cards are being selected, the number of observations is two. If the observations were independent, answer B would be correct. But the observations are not independent. If the first card is red, the probability that the second card dealt is red is 1/3. If the first card is black, the probability that the second card dealt is red is 2/3. These two probabilities would have to be the same if the observations were independent.

Practice Question 4

There are five multiple-choice questions on an exam, each with responses a, b, c, or d. Each question is worth 5 points and only one option per question is correct. Suppose a student guesses the answer to each question. His or her guesses from question to question are independent. If the student needs at least 20 points to pass the test, the probability that the student passes is closest to ______.

A. 0.0146
B. 0.0010
C. 0.0156

Correct Answer: C

X, the number correct if you were guessing, is binomial with parameters n = 5 and p = 0.25. To get at least 20 points, the student must get at least 4 of the 5 questions correct. Choice A is the probability of getting exactly 4 correct and choice B is the probability of getting exactly 5 correct. The correct answer is P(X >= 4) = P(X = 4) + P(X = 5).

Practice Question 5

For x, a random variable from a binomial distribution with N = 9 and p = 0.6, p(5) = ______ (to nearest 0.1%).

A. 27.08%
B. 25.1%
C. 1.46%

Correct Answer: B

p(5) = ₉C₅ x 0.6⁵ x 0.4⁴ = 25.1%

Practice Question 6

Which of the following is not a binomial experiment?

A. Flipping a coin 3 times and letting x count the number of heads obtained.
B. Rolling a die 3 times and letting x count the numbers of 2s obtained.
C. Randomly selecting a ball (with replacement) three times from a jar containing 1, 2, 2, 5, 6, and 7, and letting x count the number of 2s obtained.
D. Randomly selecting 3 balls from a jar containing balls numbered 1, 2, 2, 5, 6, 7 and letting x count the number of 2s obtained.

Correct Answer: D

For "randomly selecting 3 balls from a jar containing balls numbered 1, 2, 2, 5, 6, 7 and letting x count the number of 2s obtained," we do not have independent events. So, this is not a binomial experiment. We can find the probability distribution for random variable x using a tree diagram (we can not use the binomial formula).

Practice Question 7

The probability of an accident-free day at MRC is 60%. Assuming the accident-free days at MRC are independent, for a random sample of 15 days, the probability of less than 14 accident-free days is ______ (to the nearest 0.1%).

A. 4.7%
B. 99.5%
C. 0.5%

Correct Answer: B

Let X count the number of accident-free days. The events are independent with only two outcomes: an accident-free day or a day that included an accident. Binomial random variable x has N = 15 and p = 0.6. Computing the binomial distribution for binomial random variable X (using the calculator), we get P(X < 14) = 1 - P(X >= 14) = 1 - [p(14) + p(15)] = 1 - [0.0047 + 0.0004] = 1 - 0.0051 = 99.5% (to the nearest 0.1%).

Practice Question 8

Research shows that 72% of consumers have heard of MBI computers. A survey of 500 randomly selected consumers is to be conducted. What is the mean and standard deviation for the number of consumers that have heard of MBI computers?

A. 360; 10.04
B. 360; 100.80
C. 144; 100.80

Correct Answer: A

mean = 0.72 x 500 = 360
variance = 0.72 x (1 - 0.72) x 500 = 100.8
standard deviation = 100.8^1/2 = 10.04

Practice Question 9

There are five multiple-choice questions on an exam, each having responses a, b, c, or d. Each question is worth 5 points and only one option per question is correct. Suppose a student guesses the answer to each question, and his or her guesses from question to question are independent. The student's mean number of questions correct on the exam should be ______.

A. 1.25
B. 2.5
C. 6.25

Correct Answer: A

X, the number correct if you were guessing, has the binomial distribution with parameters n = 5 and p = 0.25. The mean of X is u = np = 1.25.

Practice Question 10

As part of a promotion for a new type of cracker, free trial samples are offered to shoppers in a local supermarket. The probability that a shopper will buy a packet of crackers after testing the free sample is 0.20. Different shoppers can be regarded as independent trials. Let X be the number among the next twenty shoppers who buy a packet of the crackers after tasting a free sample. The standard deviation of X is ______.

A. 4.00
B. 3.20
C. 1.79

Correct Answer: C

X, the number of shoppers who buy a packet of crackers after tasting a free sample, has a binomial distribution with parameters n = 20 and p = 0.2. The standard deviation of X is [np(1-p)]^1/2 = 1.79.

Practice Question 11

Albert is taking a 10-item multiple-choice test (4 choices per item) and randomly guessing on each item. How many items should he expect to get correct?

A. 2.5
B. 3
C. 2

Correct Answer: A

This is a binomial situation. The independent trials of the same act guessed at are item-N = 10. Each trial has exactly 2 outcomes (get item correct, get item incorrect); p, the probability of success, is 1/4. So, let random variable x count the number of items Albert gets correct and x be a random variable from a binomial experiment with N = 10 and p = 0.25. The expected value of x (the expected number of correct items) is the mean, m = Np. Here, m = (10)(0.25) = 2.5. So, Albert should expect to get 2.5 items correct.

Practice Question 12

For random variable x from a binomial distribution with N = 20 and p = 0.3, the standard deviation is ______ (to nearest 0.01).

A. 0.30
B. 4.20
C. 2.05

Correct Answer: C

The standard deviation is sqrt[Np(1 - p)]. Here, N = 20 and p = 0.3. So, the standard deviation is sqrt[(20)(0.3)(1 - 0.3)] = 2.05 (to the nearest 0.01).

Practice Question 13

Given that X is a binomial random variable, with N = 5 and p = 0.3 and that we want to find P(X < 3), which of the following is true?

A. We can approximate P(X_B < 3) with P(X_N < 2.5).
B. We can approximate P(X < 3) using a normal with mean = 1.5 and standard deviation = 1.02.
C. We cannot approximate this binomial distribution with a normal distribution.

Correct Answer: C

To approximate the binomial with a normal distribution, Np and N(1 - p) must both be greater than 5. Here, Np = (5)(0.3) = 1.5, which is not greater than 5. So, we cannot approximate P(X < 3) using a normal distribution [we would use a binomial table to find P(X < 3)].

Practice Question 14

For X, a binomial random variable with N = 70 and p = 0.3, we can approximate P(X < 19) by using a normal distribution with ______.

A. mean 70 and standard deviation 0.3
B. mean 21 and standard deviation 3.83
C. mean 70 and standard deviation 3.83

Correct Answer: B

We can approximate the binomial with a normal distribution because Np = 21 is greater than 5 and N(1 - P) = 49 is greater than 5. The normal distribution that we use to do the approximation has mean = Np = 21 and a standard deviation square root of N(p)(1 - p), in this case, 3.83 (to the nearest 0.01).

Practice Question 15

Suppose that the penalty for withdrawing funds early from a certain account follows a uniform distribution on the interval from (5%,12%). Find the expected value of the penalty.

A. 7%
B. 8.5%
C. 17%

Correct Answer: B

The expected value is (12 + 5)/2 = 8.5%.

Practice Question 16

Suppose that the penalty for withdrawing funds early from a certain account follows a uniform distribution on the interval from (5%,12%). What is the probability that the penalty is less than 7%?

A. 0.286
B. 0.416
C. 0.714

Correct Answer: A

The probability that the penalty is less than 7% is F(7) = (7 - 5)/(12 - 5) = 0.286.

Practice Question 17

MRC produces chips with a defective rate of 15%. For an random sample of 20 chips from MRC, let X count the number of defective chips in the sample (and assume x is a binomial random variable), P(X < 2) = ______ (to nearest 0.001).

A. 3.9%
B. 17.6%
C. 30%

Correct Answer: B

Binomial random variable X has N = 20 and p = 0.15. Using the calculator, we find P(X < 2) = p(0) + p(1) = 0.0387 + 0.1368 = 0.1755 = 17.6% (to the nearest 0.1%).

Practice Question 18

If an experiment results in one of two dichotomous responses, the variable is defined as a ______.

A. binomial random variable
B. discrete random variable
C. continuous random variable

Correct Answer: A

Practice Question 19

Sixty percent of the customers of a fast food chain order the Whopper, fries, and a drink. If a random sample of 15 cash register receipts is selected, what is the probability that 10 or more will show that the above three food items were ordered?

A. 0.403
B. 0.186
C. Neither of these answers

Correct Answer: A

This is a binomial probability. The probability of getting r successes out of n trials, where the probability of success of each trial is p and probability of failure of each trial is q (where q = 1 - p), is given by: n!(p^r)[q^(n-r)]/r!(n-r)!. Therefore, we need to find the probability of getting 10, 11,12,13,14,15 successes and add them up. Here, n=15, p=0.6, and q=0.4. r changes from 10 to 15.

p(10 successes) = 15!(0.6¹⁰)(0.4⁵)/10!(15-10)! = 0.1859
p(11 successes) = 15!(0.6¹¹)(0.4⁴)/11!(15-11)! = 0.1268
p(12 successes) = 0.0634
p(13 successes) = 0.0219
p(14 successes) = 0.0047
p(15 successes) = 0.00047

The sum of all the probabilities is 0.403.

Practice Question 20

David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period, 25 customers buy gasoline at this station.

What is the probability that no more than 20 pay in cash?

A. 0.1
B. 1.0
C. 0.9

Correct Answer: B

P(20) is almost zero. Probabilities of higher than 20 are also close to zero. So, the probability of not more than 20 is almost 1.

Practice Question 21

An insurance agent has appointments with 4 prospective clients tomorrow. From past experience, the agent knows that the probability of making a sale on any appointment is 1 out of 5. Using the rules of probability, what is the likelihood that the agent will sell a policy to 3 of the 4 prospective clients?

A. 0.410
B. 0.250
C. 0.026

Correct Answer: C

This is a binomial probability. The probability of getting r successes out of n trials, where the probability of success each trial is p and probability of failure each trial is q (where q = 1-p), is given by: n!(p^r)[q^(n-r)]/r!(n-r)!. Here, n = 4, r = 3,p = 0.20 and q = 0.80. Therefore, we have 4!(0.2³)(0.8¹)/3!1! = 0.026.

Practice Question 22

In a large metropolitan area, records revealed that 30 percent of all high school graduates go to college. From 20 graduates selected at random, what is the probability that exactly 8 will go to college?

A. 0.231
B. 0.114
C. 0.400

Correct Answer: B

This is a binomial probability. The probability of getting r successes out of n trials, where the probability of success each trial is p and probability of failure each trial is q (where q = 1-p), is given by: n!(p^r)[q^(n-r)]/[r!(n-r)!]. Here, n = 20, r = 8,p = 0.3 and q = 0.7. Therefore, we have 20!(0.3⁸)(0.7¹²)/[8!12!] = 0.114.

Practice Question 23

The sponsors of a well-known charity came up with a unique idea to attract wealthy patrons to a $500-a-plate dinner. After the dinner, it was announced that each patron attending could buy a set of 20 tickets for the gaming tables. The chance of winning a prize for each of the 20 plays is 50-50. If you bought a set of 20 tickets, what is the chance that you will win 15 or more prizes?

A. 0.006
B. 0.250
C. 0.021

Correct Answer: C

This is a binomial probability. The probability of getting r successes out of n trials, where the probability of success each trial is p and probability of failure each trial is q (where q = 1-p), is given by: n!(p^r)[q^(n-r)]/r!(n-r)!. Here, n = 20, p = 0.5 and q = 0.5 and r = 15,16,17,18,19,20. Therefore, we have:

P(15) = 20!(0.5¹⁵)(0.5⁵)/15!5! = 0.0148
P(16) = 20!(0.5¹⁶)(0.5⁴)/16!4! = 0.0046
P(17) = 0.0011
P(18) = 0.0002
P(19) = 0.00002
P(20) = 0.000001

The sum is 0.0207.

Practice Question 24

A trial generates only two results, "success" and "failure." The probability of success is higher than that of failure. The variance of the number of failures in 20 trials equals 2.35. The probability of success on a given trial equals ______.

A. 0.136
B. 0.864
C. 0.452

Correct Answer: B

For a binomial distribution with N trials, with the probability of success = p in each trial, the variance equals Np(1-p). Hence, 20 x p x (1 - p) = 2.35. Solving this quadratic equation gives p = 0.136 or p = 0.864.

Practice Question 25

A cup contains 4 pennies and 6 dimes. Three coins are selected with replacement from the cup. What is the probability that exactly 2 of the coins selected were pennies?

A. 0.288
B. 0.432
C. 0.712

Correct Answer: A

Since this is sampling with replacement, we use the binomial distribution with n = 3 and pai = 0.4. So, from the table, p(2) = 3!/[1! x 2!] x 0.4² x 0.6¹ = 0.288.

Practice Question 26

It is estimated that 70% of motorists on a certain stretch of highway exceed the speed limit. A highway patrolman with a radar device randomly selects 15 motorists on this part of the highway and checks their speed. What is the probability that at least 13 are caught speeding?

A. 0.092
B. 0.128
C. 0.908

Correct Answer: B

We use the binomial distribution with n = 15 and pai = 0.7 to get P(X>= 13) = p(13) + p(14) + p(15) = 0.092 + 0.031 + 0.005 = 0.128.

Practice Question 27

As part of a promotion for a new type of cracker, free trial samples are offered to shoppers in a local supermarket. The probability that a shopper will buy a packet of crackers after testing the free sample is 0.20. Different shoppers can be regarded as independent trials. Let X be the number among the next 100 shoppers who buy a packet of the crackers after tasting a free sample. X has approximately a ______.

A. N(4, 20) distribution
B. N(20, 4) distribution
C. N(0.2, 16) distribution

Correct Answer: B

The distribution is approximately normal with mean np = 20 and standard deviation [np(1-p)]^1/2 = 4.

Practice Question 28

For random variable X from a binomial random variable with parameters N and p, we can approximate a probability such as P(X < 2) with a normal distribution provided ______.

A. N > 30
B. Np < 5
C. Np > 5 and N(1 - p) > 5

Correct Answer: C

To approximate a binomial probability such as P(X < 2) with a normal distribution we must have Np > 5 and N(1 - p) > 5. Also, we can improve the approximation by making an adjustment for continuity. For P(X > 2) where x is binomial we would find P(X > 2.5) where x is normal.

Practice Question 29

The probability that the price of a stock increases is 0.30. The price of the stock will either increase or decrease each day independently of what happened on the previous day. An experiment consists of observing the price of this stock during a 30-day period. What is the probability that the stock price will increase 10 days out of the 30 days?

A. 0.03
B. 0.1416
C. 0.3333

Correct Answer: B

The number of days that the stock price increases over this period follows a binomial distribution with 30 trials, a probability of success (increase in stock price) equal to 0.30 and a probability of failure (decrease in stock price) equal to 0.70. Therefore, the parameters of the distribution are n = 30 and p = 0.3. The probability that the number of successes is 10 out of 30 trials is: p(10) = 0.1416.

Practice Question 30

The probability that the price of a stock increases is 0.30. The price of the stock will either increase or decrease each day independently of what happened on the previous day. An experiment consists of observing the price of this stock during a 30-day period. What are the expected value and the variance of the number of days that the stock price increases?

A. 6.3; 9
B. 9; 6.3
C. 9; 15

Correct Answer: B

Assume X denotes the random variable for the number of days that the stock price increases. X ~ Bin(30, 0.3) therefore, E(X) = 30 x 0.3 = 9 and V(X) = 30 x 0.3 x (1 - 0.3) = 6.3.

Practice Question 31

You are studying the finances of a life insurance company. You believe that if Company X generates at least $150 million in earnings this year, they will pay a large amount of stock into a company bonus pool. If the earnings can fall anywhere from $110 million to $165 million with equal probability, what is the likelihood they will hit the bonus pool target?

A. 27.5%
B. 27.3%
C. 26.5%

Correct Answer: B

This is a continuous uniform distribution, where b = $165 million and a = $110 million. F(x) = (x - a)/ (b - a) for a < x < b; F(x) = 0 for x <= a, and F(x) = 1 for x >= b. We are solving for 1 - F(150) = 1 - (150 - 110)/(165 - 110) = 1 - 40/55 = 27.3%.

Practice Question 32

You evaluate the monthly performance of your portfolio managers against a broad market index. At the end of each year, you add up the number of months in which their performance exceeded that of the market index. If the probability of beating the market index each month, after expenses and sales loads, is 65%, what is the mean and variance of the number of months in a year a manager would beat the index?

A. mean = 8.7; variance = 3.73
B. mean = 8.7; variance = 2.73
C. mean = 7.8; variance = 2.73

Correct Answer: C

For this problem, the number of months in a year a manager would beat the index is a binomial random variable with parameters n = 12 and p = 65%. The mean of a binomial distribution is n*p and the variance is n*p*q, where q = 1 - p. Here, we will obtain a mean of 12 * 65% = 7.8 and a variance of 12 * 35% * 65% = 2.73.

Practice Question 33

A manufacturer of headache medicine claims it is 70 percent effective within a few minutes. That is, out of every 100 users 70 get relief within a few minutes. A group of 12 patients are given the medicine. If the claim is true, what is the probability that 8 have relief within a few minutes?

A. 0.231
B. 0.667
C. 0.168

Correct Answer: A

This is a binomial probability. The probability of getting r successes out of n trials where the probability of success each trial is p and probability of failure each trial is q (where q = 1-p) is given by: n!(pr)[q(n-r)]/r!(n-r)!. Here n = 12, r = 8,p = 0.7 and q = 0.3. Therefore we have 12!(0.78)(0.34)/8!4! = 0.231.

Practice Question 34

Which of the following is false?

A. The probabilities for different possible values of a random variable with a discrete uniform distribution are equal.
B. A random variable with a binomial distribution can have one of two possible values.
C. The probabilities for different possible values of a random variable with a continuous uniform distribution are equal.

Correct Answer: B

A binomial distribution is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. It can therefore take all integer values from 0 to n.