- CFA Exams
- 2026 Level II
- Topic 7. Derivatives
- Learning Module 31. Pricing and Valuation of Forward Commitments
- Subject 2. Carry Arbitrage
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 2. Carry Arbitrage PDF Download
There are two ways to acquire an asset for use in the future.VT(T) = ST - F0(T) 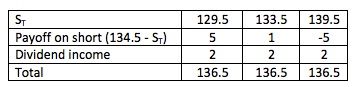
V0(T) = S0 - PV[F0(T)] S0 = PV[F0(T)], or F0(T) = FV(S0) Vt(T) = PVt,T[Ft(T) - F0(T)] Vt(T) = St - PVt,T[F0(T)] F0(T) = FV0,T[S0 + θ0 - γ0]
- First, the asset could be purchased at the spot price today and stored until it is needed.
- Second, a long position in futures could be established today and funds could be set aside in an interest-bearing account to acquire the asset in the future.
- The two strategies must have the same costs.
Pricing and Valuation at Expiration
At expiration T, the value of a forward contract to the long position is:
where:
- VT(T) is the value of the forward contract at expiration (time T).
- ST is the spot price of the underlying at T.
- F0(T) is the price of a forward contract initiated at time 0 and expiring at time T.
Example 1
An investor owns a stock that has a current value of $130. Assume that the stock will pay a $2 dividend at the end of the year. Assume that a forward contract that calls for delivery in one year is available for $134.50. The investor hedges by selling or shorting one contract.
Here are some possible outcomes:

Note that the investor shorts the forward, so VT(T) = F0(T) - ST.
A perfect hedge should return a riskless rate of return. With a perfect hedge (like the above example), the forward payoff is certain - there is no risk.
Note that the value of a forward contract can also be interpreted as its profit, the difference between what the long pays for the underlying asset, F0(T), and what the long receives, the asset price ST.
Now the question is: how do we determine F0(T) at time 0?
Pricing and Valuation at Initiation Date
The value of a forward contract at initiation (t = 0) is:
where:
- V0(T) is the value of the forward contract at initiation (time 0).
- S0 is the price of the underlying asset in the spot market at initiation (time 0).
There is no cash exchange at the beginning of the contract and hence the value of the contract at initiation is zero: V0(T) = 0. Thus,
This formula can be interpreted as saying that the forward price is the spot price compounded at the risk-free interest rate. Why?
- At time 0, we:
- buy the underlying asset at S0.
- sell a forward contract at F0(T).
The total outlay is the spot price of the asset. - We hold the asset and lose interest on the money.
- At time T, we:
- deliver the asset.
- receive the forward price for a payoff of F0(T).
The transaction is risk-free, and should be equivalent to investing S0 dollars in a risk-free asset that pays F0(T) at time T. Thus, the amount received at T must be the future value of the initial outlay invested at the risk-free rate: F0(T) = S0 (1 + r)T.
For example, suppose the spot price is $100, and the risk-free rate is 5%, and the contract is for one year. The forward price would be F0(1) = 100 (1.05)1 = 105.
Pricing and Valuation during the Life of the Contract
The value of a forward contract after initiation and during the term of the contract changes as the price of the underlying asset (S) changes. The value (profit/loss) of a forward contract between initiation and expiration is the current price of the asset less the present value of the forward price (at expiration).
Because St = PVt,T[Ft(T)]:
Why? If we went long on a forward contract at time 0 and we are now at time t prior to expiration, we hold a claim on the asset at expiration and are obligated to pay the forward price at expiration.
- The claim on the asset is worth its current spot price.
- The obligation to pay the forward price at expiration is worth the negative of its present value.
- The value of the forward contract, therefore, is the current spot price minus the forward price discounted from expiration back to the present.
Note two special circumstances:
- If t = 0, Vt(T) = V0(T) = S0 - PV0[F0(T)] = 0.
- If t = T, Vt(T) = VT(T) = ST - F0(T) = ST - F0(T).
Example 2
A three-year forward contract was established with a price of $75. Now, two years later (t = 2), the spot price is $80 and the risk-free rate is 4%. The value of the forward contract is Vt(T) = V2(3) = 80 - 75/(1.04)3-2 = 7.88.
Carry Arbitrage Model When Underlying Has Cash Flows
If we add benefits γ (dividends, interest, and convenience yield) and costs θ, the forward price of an asset at initiation becomes:
Example 3
Consider a forward contract on a 4-year bond with 1-year maturity. The current value of the bond is $1018.86. It has a face value of $1000 and a coupon rate of 10% per annum. A coupon has just been paid on the bond and further coupons will be paid after 6 months and after 1 year, just prior to delivery. Interest rates for 1 year out are flat at 8%. Compute the forward price of the bond. Assume semi-annual compounding.
F = 1018.86 x 1.042 - 50 x 1.04 - 50 = $1,000
Continuous Compounding
Assume the quoted annual rate is r, and the continuous compounding rate is rc.
- (1+r)T = ercT
- Annual compounding: FV = PV (1 + r/1)1
- Semi-annual compounding: FV = PV (1 + r/2)2
- Quarterly compounding: FV = PV (1 + r/4)4
- Continuous compounding: FV = PV erc
User Contributed Comments 0
You need to log in first to add your comment.

I am happy to say that I passed! Your study notes certainly helped prepare me for what was the most difficult exam I had ever taken.

Andrea Schildbach
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add