- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 2. Time Value of Money in Finance
- Subject 4. Cash Flow Additivity
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 4. Cash Flow Additivity PDF Download
The Cash Flow Additivity Principle is a fundamental concept in finance that states that the value of an investment portfolio is the sum of the present values of its individual cash flows. In other words, the principle asserts that the value of an investment is the sum of the present values of its expected future cash flows.
Suppose we are considering two series of cash flows (A and B). The annual interest rate is 5%. We want to know the future value of combined cash flows at t = 3.
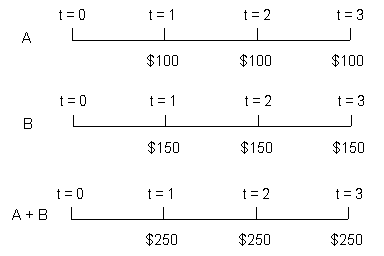
- We can calculate the future value of each series and add them up. The future value of series A is 100 x 1.052 + 100 x 1.05 + 100 = 315.25 and the future value of series B is 150 x 1.052 + 150 x 1.05 + 150 = 472.875. The future value of A + B is 788.125.
- Alternatively, we can add the cash flows of each series first and then find the future value of the combined cash flows: 250 x 1.052 + 250 x 1.05 + 250 = 315.25 = 788.125.
We can use this principle to solve many uneven cash flow problems if we add dollars indexed at the same point in time. It allows for confirmation that asset prices are the same for economically equivalent assets, even if the assets have different cash flow streams. Dollar amounts indexed at the same point in time are additive.
Consider a cash flow series, A, with $100 indexed at t = 1, 2, 3 and 5, and $0 at t = 4. This series is an almost-even cash flow, flawed only by the missing $100 at t = 4. How do we find the present value of this series?
- We can create an annuity B with $100 indexed at t = 1, 2, 3, 4, 5. It's easy to find the present value of this series.
- Then we isolate an easily evaluated cash flow B - A; it has a single cash flow of $100 at t = 4. It's also easy to find the present value of this single cash flow.
- We then subtract the present value of B - A from the present value of B.
Implied Forward Rates
Implied forward rates refer to the interest rates that are implied by the current market prices of financial instruments with different maturities.
Suppose the yields-to-maturity on a 3-year and 4-year zero coupon bonds are 3.5% and 4% on a semi-annual basis. The implied forward rate IFR6,2, can be calculated: (1 + 0.0175)6 x (1 + IFR6,2)2 = (1 + 0.02)8 => IFR6,2 = 0.0275, so the forward rate is 5.5% (0.0275 x 2). If it is greater or less than 5.5%, the cash flow additivity principle would be violated and investors would have an arbitrage opportunity.
Implied Forward Exchange Rates
The forward exchange rate is the exchange rate at which a bank agrees to exchange one currency for another at a future date when it enters into a forward contract with an investor. If the one-year risk-free interest rates are 4.2% in Canada and 4.5% in the United States and the spot CAD/USD exchange rate is 1.35, what is the one-year forward CAD/USD exchange rate that prevents investors from earning arbitrage profits?
An investment of US$10,000 would be worth US$10,000 x e0.045 = US$10,460.87
Alternatively, you can convert US$10,000 to CA$13,500 at the spot rate and investment the CA$ at 4.2%, and get CA$13,500 x e0.042 = CA$14,079.08
The implied one-year forward exchange rate must be CA$14,079.08/US$10,460.87 = 1.3459
Option Pricing
Similarly, an investor can use options to create a hedged portfolio that is risk free, irregardless of the change in the price of the underlying asset.
User Contributed Comments 17
| User | Comment |
|---|---|
| BRENDAMBITHE | YOUR study notes are simply the best although this is my first time I find them easy to understand |
| odette | I really agree with you. I couldnt read QM from the text sent to me. But i am really enjoying reading it now. |
| TammTamm | I understand this now but it would be nice to have a couple of basic questions. |
| lisalett | I don't understand the lack of sample questions. |
| Metalpro | I totally agree with BRENDAMBITHE. The notes will surely help me a lot. |
| vixignus | yeah these are good |
| VikramJ | we need questions! |
| TiredHand | Analyst Notes describes it SO MUCH BETTER THAN THE CFA textbook. |
| MNSaleem | I need help here, i am confused that through which formula The Future Value of Series A is determined, as t = 3 i expect calculation like 100 x 1.05(3) + 100 x 1.05(2) + 100. OR also i think formula for Future value of regular annunity should be used. So please some one make me clear. Thanks. |
| ybavly | @MNSaleem The diagram will make it clear. We are looking for the value AT t=3 not at the end of the year t=3. This is still an ordinary annuity. The FV here happens on t=3 which is the first day of year 3. So, we simply add the $100 because there was no time to reinvest it. |
| sgossett86 | Using the BAII+ cf key makes solving uneven cash flows very simple. |
| Chl4072 | Not understand at all How to find it by using TI..? |
| saika | Analyst Notes, you should create a tutorial for using cashflows. a small video for the calculator functions would help tremendously! Thanks. |
| shanshan34 | please upload a video. this is a little confusing thanks |
| Meruyet | The additivity principle: Dollar amounts indexed at the same point in time are additive. |
| PLF1234 | Good notes |
| Hi! Who knows how to use BA II for calculations? |

I am using your study notes and I know of at least 5 other friends of mine who used it and passed the exam last Dec. Keep up your great work!

Barnes
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add