- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 7. Estimation and Inference
- Subject 2. The Central Limit Theorem and Inference
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 2. The Central Limit Theorem and Inference PDF Download
The Central Limit Theorem
The central limit theorem states that, given a distribution with a mean μ and variance σ2, the sampling distribution of the mean x-bar approaches a normal distribution with a mean (μ) and a variance σ2/N as N, the sample size, increases.
The amazing and counter-intuitive thing about the central limit theorem is that no matter the shape of the original distribution, x-bar approaches a normal distribution.
- If the original variable X has a normal distribution, then x-bar will be normal regardless of the sample size.
- If the original variable X does not have a normal distribution, then x-bar will be normal only if N ≥ 30. This is called a distribution-free result. This means that no matter what distribution X has, it will still be normal for sufficiently large n.
Keep in mind that N is the sample size for each mean and not the number of samples. Remember that in a sampling distribution the number of samples is assumed to be infinite. The sample size is the number of scores in each sample; it is the number of scores that goes into the computation of each mean.
Two things should be noted about the effect of increasing N:
- The distributions become more and more normal.
- The spread of the distributions decreases.
Based on the central limit theorem, when the sample size is large, you can:
- use the sample mean to infer the population mean.
- construct confidence intervals for the population mean based on the normal distribution.
Note that the central limit theorem does not prescribe that the underlying population must be normally distributed. Therefore, the central limit theorem can be applied to a population with any probability distribution.
Standard Error of the Sample Mean
The standard error of a statistic is the standard deviation of the sampling distribution of that statistic.
Standard errors are important because they reflect how much sampling fluctuation a statistic will show. The inferential statistics involved in the construction of confidence intervals and significance testing are based on standard errors. The standard error of a statistic depends on the sample size. In general, the larger the sample size, the smaller the standard error. The standard error of a statistic is usually designated by the Greek letter sigma (σ) with a subscript indicating the statistic.
The standard error of the mean is designated as: σm. It is the standard deviation of the sampling distribution of the mean. The formula for the standard error of the mean is:
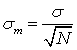
where σ is the standard deviation of the original distribution and N is the sample size (the number of scores each mean is based upon).
This formula does not assume a normal distribution. However, many of the uses of the formula do assume a normal distribution. The formula shows that the larger the sample size, the smaller the standard error of the mean. More specifically, the size of the standard error of the mean is inversely proportional to the square root of the sample size.
Example 1
Suppose that the mean grade of students in a class is 62%, with a standard deviation of 10%. A sample of 30 students is taken from the class. Calculate the standard error of the sample mean and interpret your results.
You are given that μ = 62, and σ =10. Since n = 30, the standard error of the sample mean is: σm = 10/301/2 = 1.8257. This means that if you took all possible samples of size 30 from the class, the mean of all those samples would be 62 and the standard error would be 1.8257.
Note that if you took a sample size of 50, the standard error would then be: σm = 10 / 501/2 = 1.4142.
The standard error would drop as the sample size increased, which agrees with the information above.
When sample standard deviation (s) is used as an estimate of σ (when it is unknown), the estimated standard error of the mean is s/N1/2. In most practical applications analysts need to use this formula because the population standard deviation is almost never available.
Example 2
Suppose that the mean grade of students in a class is unknown, but a sample of 30 students is taken from the class and the mean from the sample is found to be 60%, with a standard deviation of 9%. Calculate the standard error of the sample mean and interpret your results.
Now, μ and σ are unknown, but m is given as 60 and s is given as 9. Since n = 30, you can estimate the standard error of the sample mean as: 9/301/2 = 1.6432. This means that if you took all possible samples of 30 from the class, you would estimate the standard error to be 1.6432.
It is important to note that when you have σ, you must use it; when you don't, you use its sample equivalent, s.
User Contributed Comments 12
| User | Comment |
|---|---|
| achu | std error = f(s, n) |
| jpducros | Standart error formula is independant from the shape of the distribution (standart or not)....important... |
| polanki | If S is given to sample which is standard deviation of sample or standard error then why again we need to devide it by sqrt N to get sample error. |
| munro | polanki: it's the lowercase s, nor the uppercase S. |
| Raok | may I ask how to differentiate between sample size and number of sample, isn't in this case, N is sample not same size? |
| jayj001 | SAMPLE SIZE = no. of observations in each sample e.g. 100 samples with 5 observations in each NOT normal distribution as N < 30 |
| fanDango | You can have a sample size of 30 students from a population of 1000 students and also have 100 samples of 30 students. 100 is the number of samples, 30 is the sample size. |
| Bududeen | it depends if the distribution itself is not normal...if the distribution is normal , then the sample size does not affect the normality of the distribution so even with a sample size of 5, if the distribution is normal then the distribution follows a normal dist. |
| GouldenOne | What is variable X? |
| sgossett86 | Basically we're navigating from initial statistic theory to how to take our own imperfect data and make standard probability distributions so we can standardize and make inferences comparatively as an analyst. |
| Rachelle3 | its always standard deviation divided by sample (of n) I get that but when you know this then you always do it the power of 0.5? |
| mcbreatz | Power 0f .5 is same as taking the square root which is specified in the formula. |

I passed! I did not get a chance to tell you before the exam - but your site was excellent. I will definitely take it next year for Level II.

Tamara Schultz
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add