- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 5. Portfolio Mathematics
- Subject 3. Shortfall Risk and Roy's Safety-First Criterion
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 3. Shortfall Risk and Roy's Safety-First Criterion PDF Download
The focus of this section is assessing risks in a portfolio, a process that allows us to establish rules for dealing with those risks and minimize them as much as possible.
Shortfall risk is the risk that portfolio value will fall below some minimum acceptable level over some time horizon. The risk that assets in a defined benefit plan will fall below plan liabilities is an example of a shortfall risk. Therefore, shortfall risk is a downside risk. In contrast, when a risk-averse investor makes portfolio decisions in terms of the mean return and the variance (or standard deviation) of return, both upside and downside risks are considered. For example, portfolios A and B have the same mean return of 20%. The standard deviations of the returns on A and B are 5% and 8% respectively. Portfolio B has a higher risk because its standard deviation is higher. However, though the return on portfolio B is more likely to fall below 20%, it's also more likely to exceed 20%.
Safety-first rules focus on shortfall risk.
Suppose an investor views any return below a level of RL as unacceptable. Roy's safety-first criterion states that the optimal portfolio minimizes the probability that portfolio return, RP, falls below the threshold level, RL. In symbols, the investor's objective is to choose a portfolio that minimizes P(RP < RL). When portfolio returns are normally distributed, the investor can calculate P(RP < RL) using the number of standard deviations RL lies below the expected portfolio return, E(RP). The portfolio for which E(RP) - RL is largest in terms of units of standard deviations minimizes P(RP < RL). Thus, if returns are normally distributed, the safety-first optimal portfolio maximizes the safety-first ratio (SFRatio):
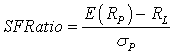
The quantity E(RP) - RL is the distance from the mean return to the shortfall level. It measures the excess return over the threshold return level. SFRatio gives the distance in units of standard deviation: it measures the excess return over the threshold level per unit of risk.
For example, the expected return on a portfolio is 20%, and the standard deviation of the portfolio return is 15%. Suppose the minimum acceptable return level is 10%. SFRatio = (20% - 10%)/15% = 0.67.
Note that the SFRatio is similar to the Sharpe ratio (E(Rp) - Rf)/standard deviation, where Rf is the risk-free rate. The SFRatio becomes the Sharpe ratio if the risk-free rate is substituted for the threshold return RL. Therefore, the safety-first criterion focuses on the excess return over the threshold return, while the Sharpe ratio focuses on the excess return over the risk-free rate.
Roy's safety-first criterion states that the optimal portfolio should minimize the probability that the rate of return of the portfolio (RP) will fall below a stated threshold level (RL). If returns are normally distributed, it states that the optimal portfolio maximizes the safety-first ratio. Therefore, assuming that returns are normally distributed, the safety-first optimal portfolio can be selected using one of the following two criteria:
- Lowest probability of RP < RL
- Highest safety-first ratio.
There are three steps in choosing among portfolios using Roy's criterion (assuming normality):
- Calculate the portfolio's SFRatio.
- Evaluate the standard normal cdf at the value calculated for the SFRatio; the probability that return will be less than RL is N(-SFRatio).
- Choose the portfolio with the lowest probability.
Example
Suppose that a certain fund has reached a value of $500,000. At the end of the next year, the fund managers wish to withdraw $20,000 for additional funding purposes, but do not wish to tap into the original $500,000.
There are three possible investment options:

Which option is most preferable? (You may assume normally distributed returns throughout.)
Answer
First, note that since the managers do not want to tap into the original fund, a return of 20000/500000 = 0.04 is the minimum acceptable return; this is the threshold return, RL.
You now need to calculate the SFRatio in each case:
A: (10-4)/15 = 0.4
B: (8-4)/12 = 0.33
C: (9-4)/14 = 0.36
You can conclude that portfolio A, with the highest SFRatio of the three, is the most preferable.
You can also take this a step further and calculate the probability that the portfolio return will fall below the threshold return, that is, P(RP < RL). To do this, we take the negative of the SFRatio in each case and find the cdf of the standard normal distribution for this value.
In symbols, P(RP < RL) = F(-SFRatio), where F is the cdf of the standard normal distribution.
From normal tables, F(-0.4) = 0.3446, F(-0.33) = 0.3707 and F(-0.36) = 0.3594.
This indicates that, for portfolio A, the chance of obtaining a return below R is 0.3446, with corresponding values for portfolios B and C of 0.3707 and 0.3594 respectively.
Since the chance of not exceeding the threshold return is lowest for portfolio A, this is again the best option.
User Contributed Comments 7
| User | Comment |
|---|---|
| surob | Why N(-SFRation)? |
| dave79 | N(-SFRatio) = 1 - N(SFratio)= P(Rp<Rl) - it is CDF probablity of return less than Rl - it is left hand -ve side of normal disrtibution curve |
| sfarrel2 | How are those cdf of the standard normal distribution amounts calculated? |
| bobert | By dividing by the standard deviation, you are getting everything standardized. Being the case, you can use the Z-table (I will show both kinds, the cumulative and normal). For the regular Z-table: F(-.4) is what you need to find. 1) .4 on the table = .1554 which is the amount beyond 0. 2) You want to find P(Rp<RL) so if you look at the bell curve, because it is a -.4 you are looking for, the area under the curve to the left of .4 std deviations to the left. 3) On a normal z-table, you are given the probability over 0 standard deviations as I mentioned. This means that the total is .5 from the left tail to 0 + .1554 to the .4 std dev. = .6554 or the p(x<.4), leaving .3446 to be p(x>.4) 4) Now you know the probability for x<.4 but you want to know p(x<-.4). Because a bell curve is symmetrical in a uniform dist, all you need to do is take 1-p(x<.4) which gives you .3446 That is for the normal z-table, using a cumulative Z-table is marginally easier for this problem. For the Cumulative Z-table: 1) Looking up .4 on the table yields .6554 Because it is cumulative, it is taking into account the negative side of the distribution already, which is why we do not need to add .5 2) If .4 encompasses all the probabilities on the left and then up to .4 std dev, to find out what is below -.4 it is simply 1-F(.4) = 1-.6554 = .3446. Remember: p(x > std dev) = p(x < -std dev) for a cumulative normal probability distribution. |
| Kobe8kenji | thanks bobert! |
| PooAn | In the above example, how is the threshold return calculated? Could you explain more about it? |
| mhdr1234 | obert... smart !!!!! |

I used your notes and passed ... highly recommended!

Lauren
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add