- CFA Exams
- 2026 Level II
- Topic 1. Quantitative Methods
- Learning Module 6. Machine Learning
- Subject 2. Overview of Evaluating ML Algorithm Performance
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 2. Overview of Evaluating ML Algorithm Performance PDF Download
Overfitting occurs when a model tries to fit the training data so closely that it does not generalize well to new data.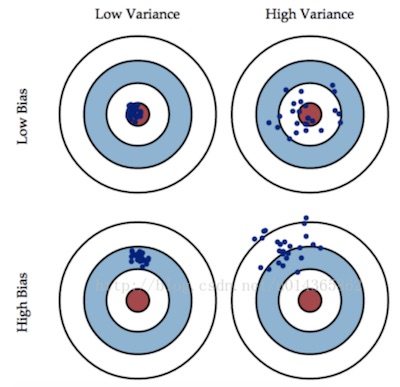
Eout = bias error + variance error + base error
The bias-variance trade-off is the point where we are adding just noise by adding model complexity (flexibility). The training error (bias error) goes down as it has to, but the test error (variance error) is starting to go up. The model after the bias-variance trade-off begins to overfit.
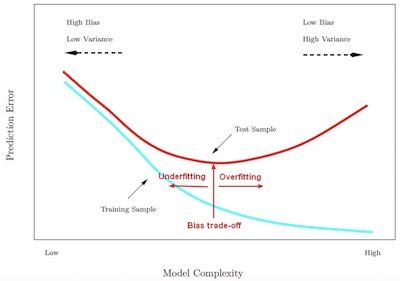
Generalization refers to the model's ability to adapt properly to new, previously unseen data, drawn from the same distribution as the one used to create the model.
There are three types of samples:
- training sample: The subset of the data set used to train a model.
- validation set: A subset of the data set - disjunct from the training set - that you use to validate the model and adjust hyperparameters.
- test set: The subset of the data set that you use to test your model after the model has gone through initial vetting by the validation set.
- It is when you create a model which is predicting the noise in the data rather than the real signal.
- Overfitting generally occurs when a model is excessively complex, such as having too many parameters relative to the number of observations.
Errors and Overfitting
In machine learning, the bias-variance tradeoff (or dilemma) is the problem of simultaneously minimizing two sources of error that prevent supervised learning algorithms from generalizing beyond their training set:
- The bias is error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting).
- The variance is error from sensitivity to small fluctuations in the training set. High variance can cause overfitting: modeling the random noise in the training data, rather than the intended outputs.

The bias-variance decomposition is a way of analyzing a learning algorithm's expected generalization error with respect to a particular problem as a sum of three terms, the bias, variance, and a quantity called the base error (irreducible), resulting from noise in the problem itself.

Preventing Overfitting
There are two common principles:- Complexity reduction: simple algorithms, limit the number of features, etc to keep things simple.
- Avoid sampling bias: K-fold-cross-validation technique can be used to mitigate the holdout sample problem (excessive reduction of the training set size).
User Contributed Comments 0
You need to log in first to add your comment.

You have a wonderful website and definitely should take some credit for your members' outstanding grades.

Colin Sampaleanu
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add