- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 6. Simulation Methods
- Subject 1. Lognormal Distribution and Continuously Compounding
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 1. Lognormal Distribution and Continuously Compounding PDF Download
The Lognormal Distribution
Some of the key properties of normal distribution are:
- It is symmetrical about the mean.
- It has zero skewness.
- It has a kurtosis of 3.
A random variable, Y, follows a lognormal distribution if its natural logarithm, lnY, is normally distributed. You can think of the term lognormal as "the log is normal." For example, suppose X is a normal random variable, and Y = eX. Therefore, LnY = Ln(eX) = X. Because X is normally distributed, Y follows a lognormal distribution.
- Like the normal distribution, the lognormal distribution is completely described by two parameters: mean and variance.
- Unlike the normal distribution, the lognormal distribution is defined in terms of the parameters of the associated normal distribution. Note that the mean of Y is not equal to the mean of X, and the variance of Y is not equal to the variance of X. In contrast, the normal distribution is defined by its own mean and variance.
- The lognormal distribution is bounded below by 0. In contrast, the normal distribution extends to negative infinity without limit.
- The lognormal distribution is skewed to the right (i.e., it has a long right tail). In contrast, the normal distribution is bell-shaped (i.e., it is symmetrical).
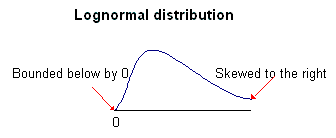
The reverse is also true; if a random variable Y follows a lognormal distribution, then its natural logarithm, lnY, is normally distributed.
Continuously Compounded Rates of Return
A discretely compounded rate of return measures the rate of changes in the value of an asset over a period under the assumption that the number of compounding periods is countable. Most standard deposit and loan instruments are compounded at discrete and evenly spaced periods, such as annually or monthly. For example, suppose that the holding period return on a stock over a year is 50%. If the rate of return is compounded on a quarterly basis, the compounded quarterly rate of return on the stock is (1 + 0.5)1/4 - 1 = 10.67%.
The continuously compounded rate of return measures the rate of change in the value of an asset associated with a holding period under the assumption of continuously compounding. It is the natural logarithm of 1 plus the holding period return, or equivalently, the natural logarithm of the ending price over the beginning price. From t to t + 1:
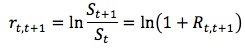
S: stock price. Rt, t + 1: the rate of return from t to t + 1
Example 1
S0 = $30, S1 = $34.50. ==> Rt, t + 1 = $34.50/$30 - 1 = 0.15, and r0, 1 = 0.139762. The continuously compounded return is smaller than the associated holding period return.
Example 2
Assume that a particular stock has a price of $200 at the start of a period and a price of $250 at the end of that period. That is, S0 = 200, and S1 = 250.
Hence, R, the holding period return, is: R = [S1/ S0] - 1 = [250/200] - 1 = 25%.
Using the formula for the continuously compounded rate of return gives: ln(1+R) = ln(S1/ S0) = ln(1.25) = 0.223 or 22.3%.
In order to see why the latter is preferable, consider the following:
Suppose that the stock now falls from $250 to $200. Then, R = [200/250] - 1 = -0.2 or -20%. So, effectively, the stock has returned to its original price, but combining the two rates of return and averaging them gives [(0.25+ (-0.2)] / 2 = 0.05 / 2 = 0.025 or 2.5%, which is misleading, as in actual fact the stock has returned to its original price, and hence the return is effectively 0%.
However, ln(1+R) = ln[(1 + (-0.2)] = ln(0.8) = -0.223 or -22.3%, which is exactly the negative of the original return. Averaging these two rates gives [(0.223 + (-0.223)] / 2 = 0 / 2 = 0 or 0%, which is the true rate of return for the period.
Thus, a continuously compounded return gives a more accurate account of the true picture of the rate of return over a period.
User Contributed Comments 16
| User | Comment |
|---|---|
| surob | Perfect explanation why continuosly compounded return is better than HPY. Good job!!! |
| achu | That is a good explanation of why Cnts compouding is better. I wonder if it's used in the real world, though. |
| rufi | this is a good tool for BSOPM |
| bahodir | what is BSOPM? |
| bobert | Black-Scholes Option Pricing Model |
| aakash1108 | nice. |
| Seemorr | What kind of variable would be lognormally distributed, but not normally? |
| riouxcf | Some variables which have frequent outliers can be made more normal by taking the log. The normal distribution tends to underestimate extremes. |
| jpducros | Is Continuously coumpounding yield always < HPY ? More generally, can we always write : Cont Compound Y < HPY < MMY < BEY < EAY And is BEY = BDiscountYield ? So many Yields it becomes complicated to remember everything, and the logic behind. |
| pbielstein | You should keep in mind though that in this example the arithmetic average for the discretely compounded returns is taken. If you take the geometric average then you obtain sqrt{(1-0.2)*(1+0.25)} - 1 = 0 |
| czar | Seemor: stock prices (log) and stock returns (normal) as stock prices lowest value can only be 0 while returns can be negative |
| johntan1979 | Shouldn't the discretely compounded quarterly rate of return = (1 + HPR/4)^4 ? 1, not (1 + HPR)^1/4 - 1? |
| johntan1979 | How can the quarterly compounding be less than the annual HPR? |
| fanDango | The quarterly compounding rate is not 4*X = annual HPR because you are compounding the principle and interest each quarter. |
| Streberli | @riouxcf lognormal distributions can't go negative they are used in stockprices not returns. what you mean is student-t distribution with this one you can include the fat tails in of return distributions |
| bcgomes786 | no mention of Volatility? these notes are not complete |

I was very pleased with your notes and question bank. I especially like the mock exams because it helped to pull everything together.

Martin Rockenfeldt
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add