- CFA Exams
- 2026 Level II
- Topic 1. Quantitative Methods
- Learning Module 1. Basics of Multiple Regression and Underlying Assumptions
- Subject 2. A Multiple Linear Regression Example
Seeing is believing!
Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.
Subject 2. A Multiple Linear Regression Example PDF Download
The population parameters β0, β1, ..., βk are unknown and are estimated using a sample of T observations on the dependent variable Y and the K independent variables X1t, X2t, ... , Xkt. Once we have estimated the parameters β0, β1, ..., βk, we obtain an estimated regression equation, which is called the sample regression equation.
The value b0 is the sample estimate of the population parameter β0, the value b1 is the sample estimate of the population parameter β1, and so forth. The value y-hatt is called the fitted value of Yt or the predicted value of Yt.
Example
It is reasonable to suspect that gasoline mileage for a car is determined mainly by the car's weight and engine size. We decided to estimate the regression
where
- Yt = the gasoline mileage (in miles per gallon) of the t-th car.
- X1t = the engine size of the t-th car (in hundreds of cubic inches).
- X2t = the weight of the t-th car (in tons).
The following table shows the results of this linear regression using a sample of T = 10 different cars.
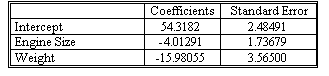
Therefore, we obtain the estimated equation (after rounding) of y-hatt = 54.3182 - 4.0129X1t - 15.9806X2t
The predicted mileage for a car that has a 2.4-hundred-cubic-inch engine and weighs 0.9 ton is obtained by substituting the values X1t = 2.4 and X2t = -0.9 into the estimated equation. The predicted value is then 54.3182 - 4.0129 (2.4) - 15.9806 (0.9) = 30.3047, or about 30.3 miles per gallon.
The standard error column gives the standard error (the standard deviation) of the estimated regression coefficients.
We have T = 10 observations and k = 2 explanatory variables in the model, so the appropriate degrees of freedom is 10 - 2 - 1 = 7.
User Contributed Comments 0
You need to log in first to add your comment.

I just wanted to share the good news that I passed CFA Level I!!! Thank you for your help - I think the online question bank helped cut the clutter and made a positive difference.

Edward Liu
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add