An AR(1) series is said to be covariance stationary if the absolute value of the lag coefficient b₁ is less than 1. If the absolute value of b₁ = 1, the time series is said to have a unit root.

All random walks have unit roots since they have b₁ = 1. This implies that they are not covariance stationary; hence we cannot apply the standard linear regression to test for b₁ = 1.

First Differencing

If we believe a time series is a random walk i.e. has a unit root, we can transform the data to a covariance stationary time series using a procedure called First Differencing. It involves subtracting the dependent variable in the immediately preceding period from the current value of the time series to define a new dependent variable, y.

Note that by taking first differences, you model the change in the value of the dependent variable. AR(1) y_t = b₀ + b_ty_t-1 + ε_t

If b₀ = b₁ = 0, then y_t = ε_t and ε_t = x_t - x_t-1, then y_t = x_t - x_t-1 = ε_t

This transformed time series has a finite mean reverting level of b₀/(1 - b₁) = 0 and is therefore covariance stationary.

This is how first differencing removes the upward trend.

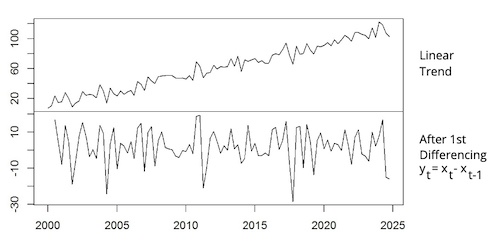
A properly differenced random walk time series is covariance stationary with a mean reversion level of 0.

The Unit Root Test for Nonstationary

If an AR (1) model has a coefficient of 1, it has a 'unit root' and no finite mean reverting level i.e. it is not covariance stationary. By definition, all Random Walks with or without a drift term have unit roots. Dickey and Fuller (DF) transform the AR (1) model to run a simple regression.

Rather than directly testing whether the original coefficient is different from 1, they test whether the new transformed coefficient (b₁ - 1) is different from 0 using a modified t-test. In their actual test, Dickey and Fuller use the variable g = b₁ - 1.

H₀: g = 0. Time series has Unit Root (Not Stationary)

H₁: g < 0. Time series doesn't have a Unit Root (Stationary).

If g is not significantly different from 0, then b₁ = 0, the series must have a unit root. The null hypothesis will be rejected if the time series does not have a unit root. On the other hand, failure to reject the null hypothesis means that the time series has a unit root.