- CFA Exams
- CFA Level I Exam
- Topic 6. Fixed Income
- Learning Module 28. Valuation and Analysis of Bonds with Embedded Options
- Subject 3. Valuation of Default-Free Callable and Putable Bonds
CFA Practice Question
What is the value of a 2-year, 6% coupon, callable bond (in one year at 100) given the following interest rate tree?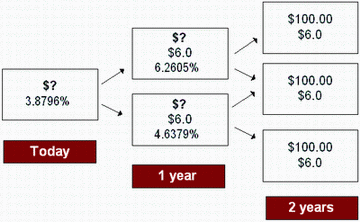

Correct Answer: 101.923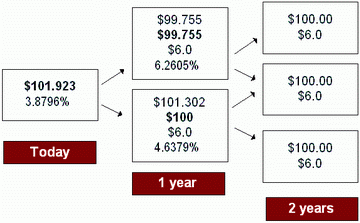

Current value of the bond at node 0 = [(99.755 + 6) / (1.038796) + (100.000 + 6) / (1.038796)] / 2 = 101.923
User Contributed Comments 14
| User | Comment |
|---|---|
| katybo | finally Im understanding binomial trees! |
| xyzanand | Life is a binomial tree... |
| octavianus | How do you calculate the call values in general? In this case, how do you determine $99.755 (Up) and $100 (down) for year 1 call values? Please help!!!! |
| mchu | Value at the Node = Min {Value from backward induction, Call price} Call price is par. |
| tabulator | octavianus, take some time reading notes and not jumping straigh to problems |
| rhardin | Yes, the notes were very clear and helpful. Read them. |
| moghizz | read them octavianus! read them! |
| charomano | 99.755 = 0.5*(100+6)/(1+0.06205) + 0.5*(100+6) / (1+0.06205) |
| ukrainia | Octavianus check the notes brah! |
| ybavly | Jeez, Octavianus, it's right there staring at you. Read the notes!! |
| bbadger | If the interest rate is less than the coupon rate, write in the call value. You need a greater than coupon interest rate to discount to less than par value. |
| bbadger | And don't read the notes Octa, in fact I hope at least 65% of you don't study at all. Thanks. |
| thebkr777 | ^LOL @bbadger Level 2 thinking right here |
| davidt876 | ...turns out octa really doesn't have a clue wa gwaan |
