- CFA Exams
- CFA Level I Exam
- Topic 1. Quantitative Methods
- Learning Module 8. Hypothesis Testing
- Subject 7. Test of a Single Mean
CFA Practice Question
A hypothesis test at the 5% level of significance, where the population standard deviation is 5.5, is constructed. A random sample of size n = 18 yields a sample mean of 67 and a sample standard deviation of 6. The critical value for H0: μ > 70 is ______.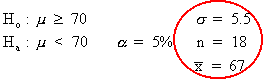
B. -1.645
C. 1.740
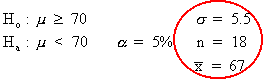
A. -1.740
B. -1.645
C. 1.740
Correct Answer: B
Because the population standard deviation, σ, is known to be 5.5, we use a normal distribution, z(0.05). Looking in the normal table for 0.05 and reading back to the row and column, we get -1.645. The rejection region is to the bottom 5%, so the critical value is -1.645.
User Contributed Comments 10
| User | Comment |
|---|---|
| oluji | why use the z table here when the sample size is less than 30 and the population is not stated as normal. I assumed the t-table is the appropriate tool. Can someone enlighten me? |
| jade | z-test should be used as the population variance (standard deviation) is known! |
| sapphire | Does anybody know how to get -1.645 from the table? What I get is 0.5199. Thanks a lot! |
| StanleyMo | hello sapphire, in fact this consider as two tails test with 5% critical percen at right and left, so for total 10% critial percen it was 1.645. ( 90% confidence interval) |
| afficionado | Oluji, when the distribution is normal and the population variance is known, regardless of the sample, the appropriate statistic is z |
| johntan1979 | The question never stated that the distribution is normal. t test is more appropriate for n<30 |
| gill15 | agree -- t test --- this is not right.. |
| Shaan23 | Agree with John and Gill. Both have are always spot on when it comes to this stuff. |
| Shaan23 | Actually John and Gill are incorrect here but this question is written poorly. It doesnt state that it is normally distributed but cause three answers do appear -- we have to assume its normal. If we assume its non-normal also, because the n<30 we would not be able to do T-test or Z-test because they require N>30 for both if NON-NORMAL. From this logic, since it is normal and we know standard deviation --- use Z test. |
| lawlee | how do we know the rejection region is the top of bottom 5%? Anyone please. |
