- CFA Exams
- CFA Level I Exam
- Topic 6. Fixed Income
- Learning Module 27. The Arbitrage-Free Valuation Framework
- Subject 3. Valuing an Option-Free Bond with a Binomial Tree
CFA Practice Question
Given the interest rate tree below, what is the price of a three-year, annual-coupon bond with a coupon rate of 4% and par value of $100?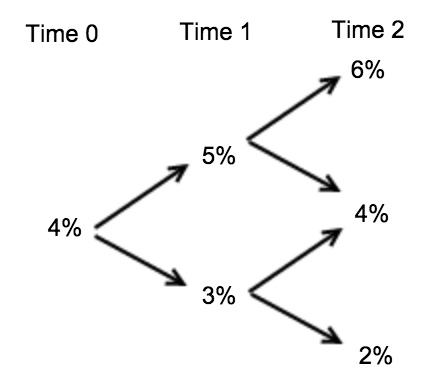

Correct Answer: 100.0345
[104/1.06+ 104/1.06] x 0.5 + 4 = 102.1132
[104/1.04+ 104/1.04] x 0.5 + 4 = 104
[104/1.02+ 104/1.02] x 0.5 + 4 = 105.9608
[102.1132/1.05+ 104/1.05] x 0.5 + 4 = 102.1491
[104/1.03+ 105.9608/1.03] x 0.5 + 4 = 105.9227
At time 2 we have the following values:
[104/1.06+ 104/1.06] x 0.5 + 4 = 102.1132
[104/1.04+ 104/1.04] x 0.5 + 4 = 104
[104/1.02+ 104/1.02] x 0.5 + 4 = 105.9608
At time 1 we have the following values:
[102.1132/1.05+ 104/1.05] x 0.5 + 4 = 102.1491
[104/1.03+ 105.9608/1.03] x 0.5 + 4 = 105.9227
At time 0: [102.1491/1.04+ 105.9227/1.04] x 0.5 + 4 = 100.0345
User Contributed Comments 4
| User | Comment |
|---|---|
| philjoe | three year bond with 4 coupons? |
| myron | @philjoe: The end of year 3's values are know for certain ($104). Given the interest rate at t = 2 (end of year 2) we can calculate the value at the end of year 2... |
| ashish100 | s math up there.. at time 0 calc doesnt add up right |
| davidt87 | they "+4" shouldnt be there at time 0. i really don't like how they've laid out the calculations. the coupon is added when discounting, not after discounting. they make it look like the coupon is missing from the price which isn't the case, and leads to stupid mistakes like the last line of the calculation |
